|
|
以前都是用MATLAB或是EXCEL给学生讲资产组合的计算问题,实际R语言也可以做一样的事情。资产组合要解决的问题并不复杂,即给定一个可选的资产集合,要从中选择出一个最优组合,使其收益率较大,而风险较小。如果可选资产只有两个的话,问题非常简单,可以通过求导最优化的方式得到结果,即有效资产前沿的解析解。如果资产集合超过两个那么问题要复杂一些。首先需要给定一个要求的期望收益率,再求出在此约束下的方差最小组合,这可以通过二次规划解出。这样得到有效前沿上的一个点。然后更改期望收益率,又可以得到另一个最优解,如此反复即可得到多资产组合的有效前沿。
下面我们先用R语言中quadprog包的二次规划求解函数来计算一个例子,再用fPortfolio包中的函数来完成同样的任务。例子中使用的数据来自于fPortfolio包中的SMALLCAP.RET数据集,使用了其中的四个资产来示例。- library(quadprog)
- library(fPortfolio)
- data <- SMALLCAP.RET[, c("BKE", "GG", "GYMB", "KRON")]
- # 计算得到收益率数据的协方差矩阵和期望
- sigma <- covEstimator(data)$Sigma
- mu <- covEstimator(data)$mu
- # 计算给定期望收益率为0.03条件下的最优组合,且不可作空
- A <- cbind(rep(1, 4), mu,diag(rep(1, 4))) #约束系数
- D <- sigma # 协方差矩阵
- x <- mu # 期望收益
- b <- c(1, 0.03, 0,0,0,0) #约束的右侧值
- res <- solve.QP(2 * D, x, A, b, meq=2)
- round(res$solution,2)
- # 设定组合的期望收益率为0.03
- spec <- portfolioSpec(portfolio=list
- (targetReturn=0.03))
- # 设定组合的约束不许做空
- cons <- 'LongOnly'
- # 求解
- res <- efficientPortfolio(data, spec = spec,
- constraints = cons)
- summary(res)
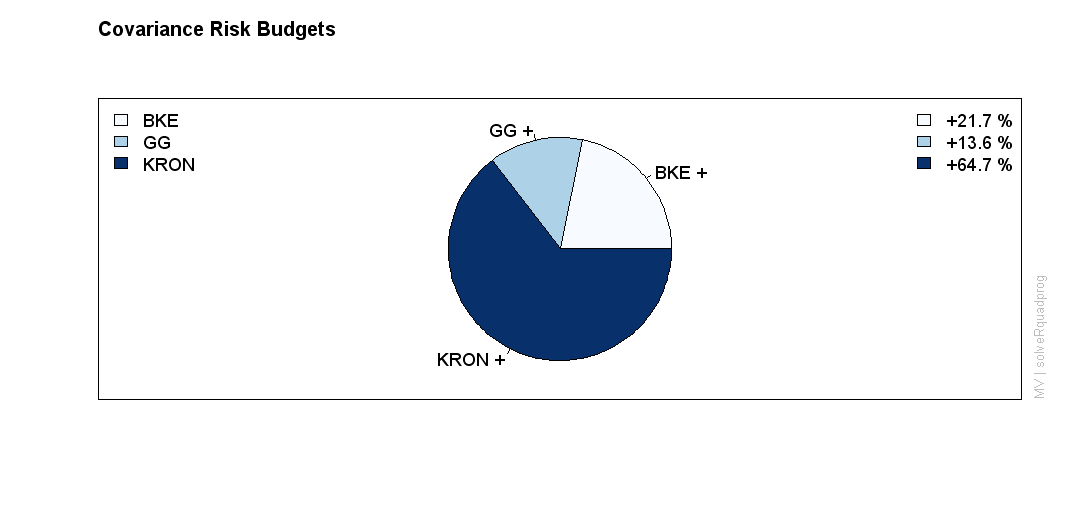
存在res中的输出结果非常丰富,其中包括了最优组合的权重,以及在此权重下的组合期望收益率和组合标准差,此外还提供了组合的风险价值VaR和条件风险价值CVaR。输出中的风险预算表示各资产对组合风险的贡献比例,可见KRON所占风险最高。我们还可以计算出有效前沿上的所有组合并绘制成图。- spec <- portfolioSpec(portfolio=list
- (nFrontierPoints = 100,
- riskFreeRate=0.01))
- # 计算有效前沿,并不许做空
- frontier <- portfolioFrontier(data,spec=spec,
- constraints = cons)
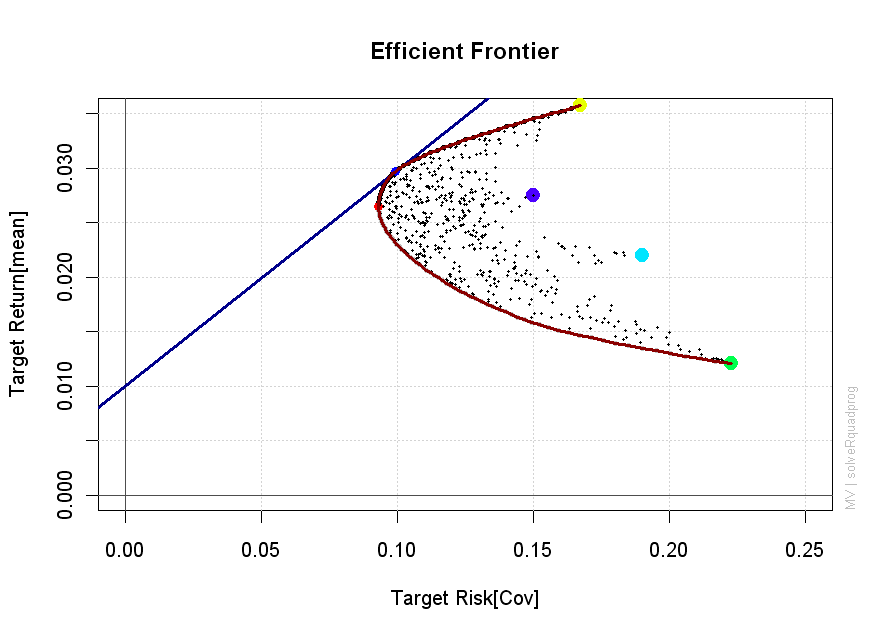
- # 有效前沿绘图
- frontierPlot(frontier,
- pch = 19,
- cex = 0.5,
- xlim=c(0,0.25),
- ylim=c(0,0.035))
- grid()
- abline(h = 0, col = "grey30")
- abline(v = 0, col = "grey30")
- minvariancePoints(frontier, pch = 19, col = "red")
- tangencyPoints(frontier, pch = 19, col = "blue")
- tangencyLines(frontier, col = "darkblue",lwd=3)
- singleAssetPoints(frontier, pch = 19, cex = 1.5, col = topo.colors(6))
- front <- frontierPoints(frontier)
- monteCarloPoints(frontier, mcSteps = 500, pch = 19,
- cex = 0.3)
- lines(front, col = "red4", lwd = 3)
原址http://www.tuicool.com/articles/BzUria |
|